| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 트리
- AIFFEL
- 힙
- ssac
- 힙구조
- 분할정복
- 다이나믹프로그래밍
- 퍼셉트론
- 자료구조
- memoization
- 아직
- 우선순위큐
- Image Classification
- 스티커
- tree
- 머신러닝
- 오차역전파법
- 인공지는
- 딥러닝
- 인공지능
- 메모이제이션
- 피보나치수열
- 피보나치
- dp
- 알고리즘
- 역전파
- 병합정렬
- 밑시딥
- 어렵다
- Today
- Total
딥러닝 for Deep Learning
밑.시.딥. Chapter2. 퍼셉트론(Perceptron) 본문
[퍼셉트론]
퍼셉트론:
프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 고안한 알고리즘.
신경망(딥러닝)의 기원이 되는 알고리즘.
퍼셉트론이란?
퍼셉트론은 다수의 신호를 받아 하나의 신호를 출력.
신호: 전류나 강물처럼 흐름이 있는 것
- 흐른다: 1
- 안 흐른다: 0

- x1, x2: 입력 신호
- y: 출력 신호
- w1, w2: 가중치(weight)
위 그림 중, 원을 뉴런 혹은 노드라고 하며, 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다.
가중치와 곱해진 입력 신호가 정해진 한계(임계값(θ) )를 넘어설 때만 1을 출력한다.
수식은 아래와 같다.

단순한 논리 회로
AND 게이트
입력이 둘이고 출력은 하나인 게이트
두 입력이 모두 1일 때만 1을 출력, 아니면 0

위 조건을 만족하는 매개변수 조합
| w1 | w2 | θ |
| 0.5 | 0,5 | 0.7 |
| 0.5 | 0.5 | 0.8 |
| 1.0 | 1.0 | 1.0 |
x1, x2 모두가 1일 때만 가중 신호의 총합이 임계값을 넘어선다.
NAND 게이트
Not AND
AND 게이트의 출력의 반대.
두 입력이 모두 1일 때만 0을 출력, 아니면 1

| w1 | w2 | θ |
| -0.5 | -0,5 | -0.7 |
OR게이트
입력 신호중 하나 이상이 1이면 1을 출력, 하나도 없으면 0

퍼셉트론의 구조는 위 세가지 게이트 모두에서 같다.
바뀌는 것은 가중치와 임계값 뿐이다.
퍼셉트론 구현하기
AND 게이트 구현

가중치와 편향 도입
임계값 θ 를 -b로 치환

- b: 편향(bias)
- w1, w2: 가중치(weight)
입력 신호에 가중치를 곱한 값에 편향을 합하고, 그 값이 0을 넘으면 1을 출력, 아니면 0.
다시 구현
AND 게이트

NAND 게이트

OR 게이트

가중치(w1, w2): 각 입력 신호가 결과에 주는 영향력(중요도)을 조정하는 매개변수
편향(bias): 뉴런이 얼마나 쉽게 활성화 (결과로 1을 출력)하느냐를 조정하는 매개변수
퍼셉트론의 한계
XOR 게이트
XOR 게이트(eXclusive OR)는 배타적 논리합이라는 논리 회로.
'배타적'이란 자기외에는 거부한다는 의미.
두 입력 중 한쪽이 1일 때만 1을 출력.

지금까지의 퍼셉트론으로는 XOR 게이트를 구현할 수 없다.
예시로, OR 게이트는 가중치 매개변수 {(b, w1, w2) = (-0.5, 1.0, 1.0)} 일 때 아래의 진리표를 만족한다.

식으론 아래와 같이 표현된다.

위 식은 직선으로 나뉜 두 영역을 만든다.
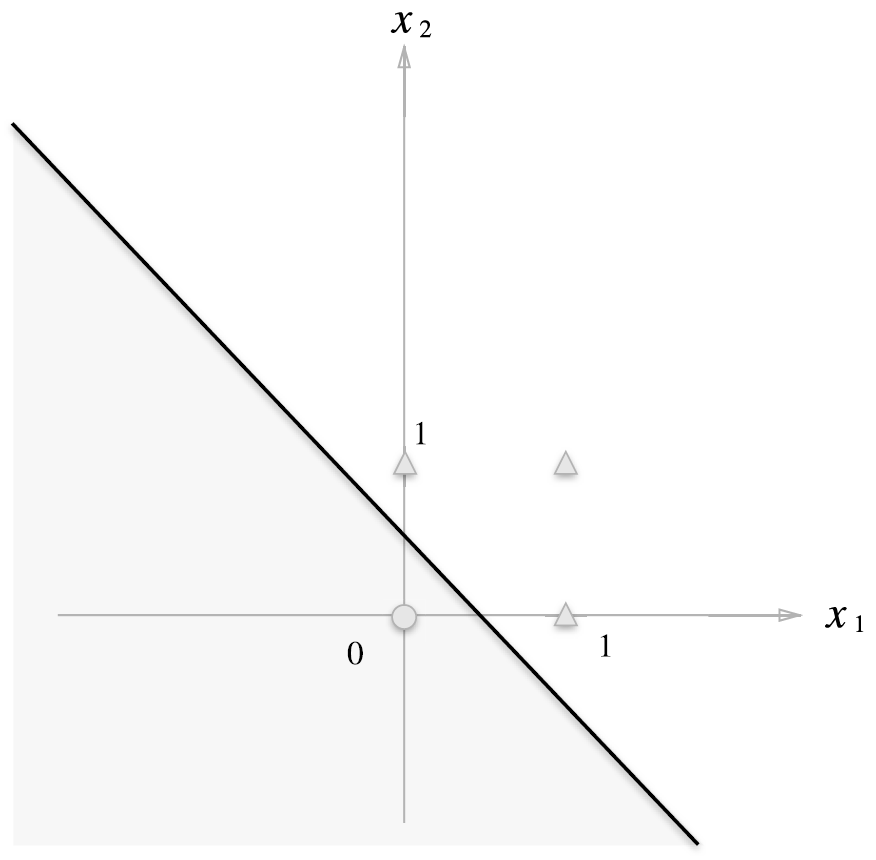
네 점을 직선으로 잘 나누고 있다.
그러나 XOR 게이트의 경우는?
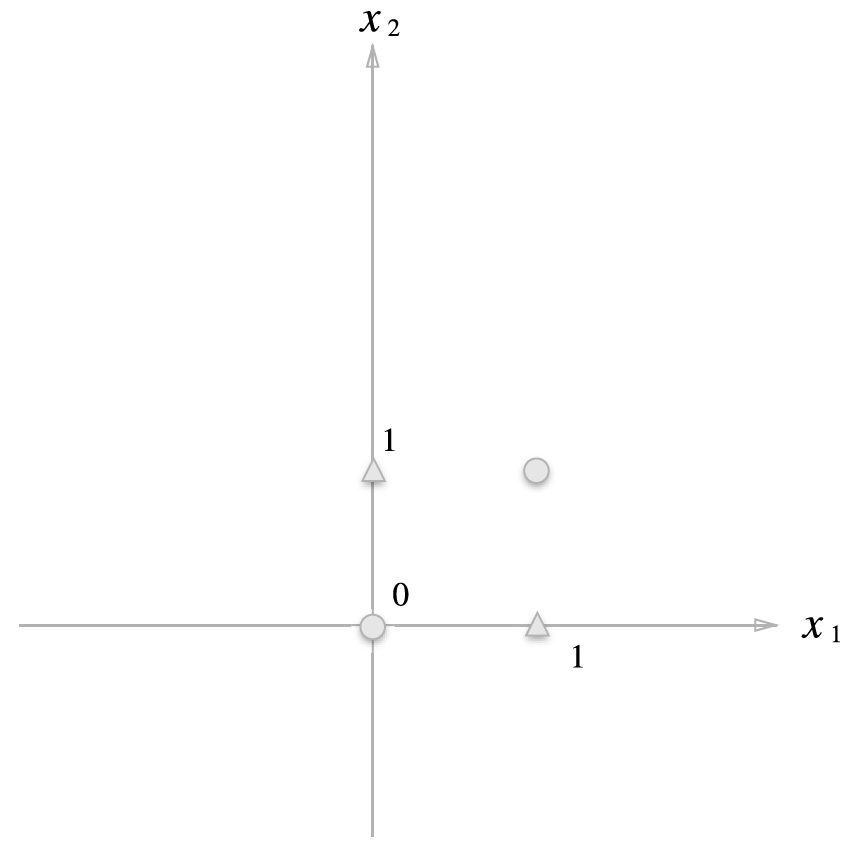
직선 하나로는 어떤 식으로도 동그라미와 세모 점을 구분할 수가 없다.
선형과 비선형
그치만 '직선'이 아니라면?

곡선의 영역을 비선형 영역
직선의 영역을 선형 영역
다층 퍼셉트론이 출동한다면
퍼셉트론을 여러층으로 쌓아 다층 퍼셉트론(multi-layer perceptron)을 만들면 XOR 게이트도 표현할 수 있다.
기존 게이트 조합하기
AND, NAND, OR 게이트를 조합해서 XOR 게이트를 만든다.

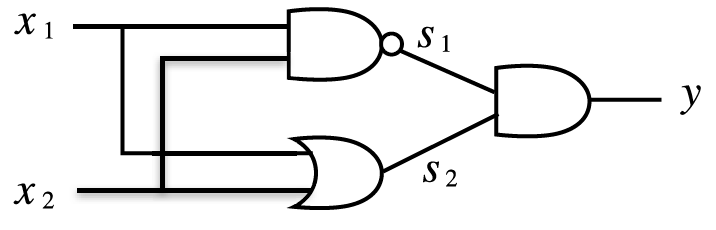
- x1, x2: NAND와 OR 게이트의 입력
- s1, s2: NAND와 OR 게이트의 출력

XOR 게이트 구현하기


AND, OR 은 단층 퍼셉트론
XOR은 2층 퍼셉트론
층이 여러 개인 퍼셉트론을 다층 퍼셉트론이라 한다.
NAND에서 컴퓨터까지
다층 퍼셉트론을 가능성은 무궁무진.
덧셈을 처리하는 가산기, 2진수를 10진수로 변환하는 인코더, 조건을 만족하면 1을 출력하는 회로 등...
심지어 NAND 게이트의 조합만으로 컴퓨터를 만들 수도 있다. 놀랍다.
비선형인 시그모이드 함수를 활성화 함수로 이용하면 임의의 함수를 표현할 수 있다는 사실이 증명됨.
정리
- 퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- 퍼셉트론에서 '가중치'와 '편향'을 매개변수로 설정한다.
- 퍼셉트론으로 AND. OR 게이트 등의 논리 회로를 표현할 수 있다.
- XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
- 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.
- 단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.
- 다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.
자료출처:
밑바닥부터 시작하는 딥러닝 1 - 사이토 고키 저
'지하에서부터 시작하는 딥러닝' 카테고리의 다른 글
| 밑.시.딥. Chapter8. 딥러닝 (0) | 2021.09.01 |
|---|---|
| 밑.시.딥. Chapter5. 오차역전파법(Backpropagation) (0) | 2021.08.11 |
| 밑.시.딥. 2 - 4장 word2vec 속도개선 part2 (0) | 2021.02.14 |
| 5장 오차역전파법 part2 (0) | 2021.01.26 |




